내분점과 외분점 공식에 대해 알아보겠습니다. 이 두 개념은 기하학에서 매우 중요한 역할을 하며, 특히 선분을 나누는 방법에 대한 이해를 돕습니다. 이번 포스팅에서는 내분점과 외분점의 정의부터 시작하여, 각각의 공식과 활용 예시까지 자세히 설명하겠습니다.
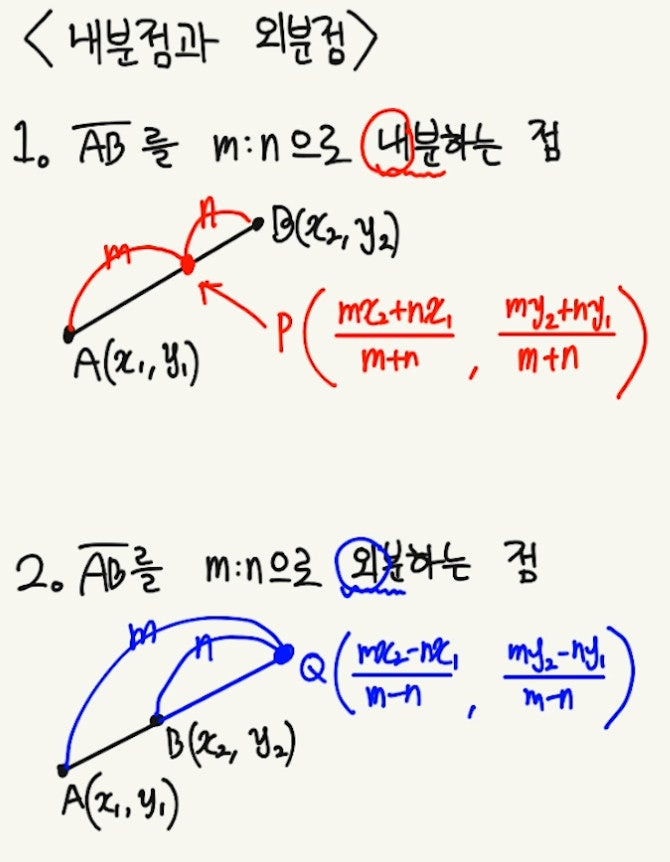
내분점은 선분의 두 끝점 사이를 특정 비율로 나누는 점을 의미합니다. 예를 들어, 선분 AB가 있을 때, 점 P가 AB를 m:n의 비율로 나눈다면, P는 내분점입니다. 반면, 외분점은 선분의 연장선상에 위치하여 두 점을 특정 비율로 나누는 점을 의미합니다. 즉, 점 Q가 AB의 연장선 위에 위치하며, AQ:QB = m:n일 때, Q는 외분점입니다.

내분점 공식
내분점 P의 좌표는 다음과 같은 공식을 통해 구할 수 있습니다.
[ P\left(\frac\right) ]
이 공식은 외부에서 선분을 나누는 점의 좌표를 구하는 데 사용됩니다. 이때 m과 n은 양수여야 하며, m이 n과 같지 않아야 합니다.

내분점과 외분점의 차이점
내분점과 외분점의 가장 큰 차이는 위치에 있습니다. 내분점은 선분의 내부에 위치하는 반면, 외분점은 선분의 연장선상에 위치합니다. 또한, 내분점은 두 점을 나누는 비율이 항상 양수인 반면, 외분점은 비율이 음수일 수 있습니다. 이러한 차이점은 기하학적 문제를 해결하는 데 중요한 요소가 됩니다.

내분점과 외분점의 활용 예시
내분점과 외분점은 다양한 기하학적 문제에서 활용됩니다. 예를 들어, 건축 설계나 그래픽 디자인에서 특정 비율로 선을 나누는 경우, 이 공식을 사용하여 정확한 위치를 계산할 수 있습니다. 또한, 물리학에서는 힘의 분배를 계산할 때도 이러한 개념이 사용됩니다.
정리 및 참고 자료
내분점과 외분점은 기하학에서 매우 중요한 개념으로, 이 두 점을 이해하고 활용하는 것은 다양한 분야에서 유용합니다. 더 자세한 내용은 아래의 링크를 참고하시기 바랍니다.

이 포스팅이 내분점과 외분점에 대한 이해를 돕는 데 도움이 되었기를 바랍니다. 기하학적 문제를 해결하는 데 있어 이 두 개념을 잘 활용하시기 바랍니다.
